DSA was HARD until I Learned these 20 Patterns

Templates included

I’ve solved over 2,000 coding problems across LeetCode and other platforms, and if there’s one thing I’ve learned, it’s this:

Getting good at DSA is less about how many problems you solve and more about how many patterns you truly understand.

Patterns help you solve a wide range of problems in less time because they train you to recognize the right approach, even for questions you have never seen before.

In this article, I’ll walk you through the 20 most important patterns that made learning DSA and preparing for coding interviews far less painful for me.

Even better, these are the same patterns that showed up again and again in my interviews, including at companies like Amazon and Google.

For each pattern, I’ll share:

• When to use it

• A reusable template

• A sample problem walkthrough

• Practice links to related LeetCode problems

This article is the essence of everything I have learned about DSA and LeetCode, distilled into one guide. I’ve also added links for each pattern so you can dive deeper when you’re ready.

If you want to explore more patterns and resources, check out: algomaster.io

Let’s get started.

---

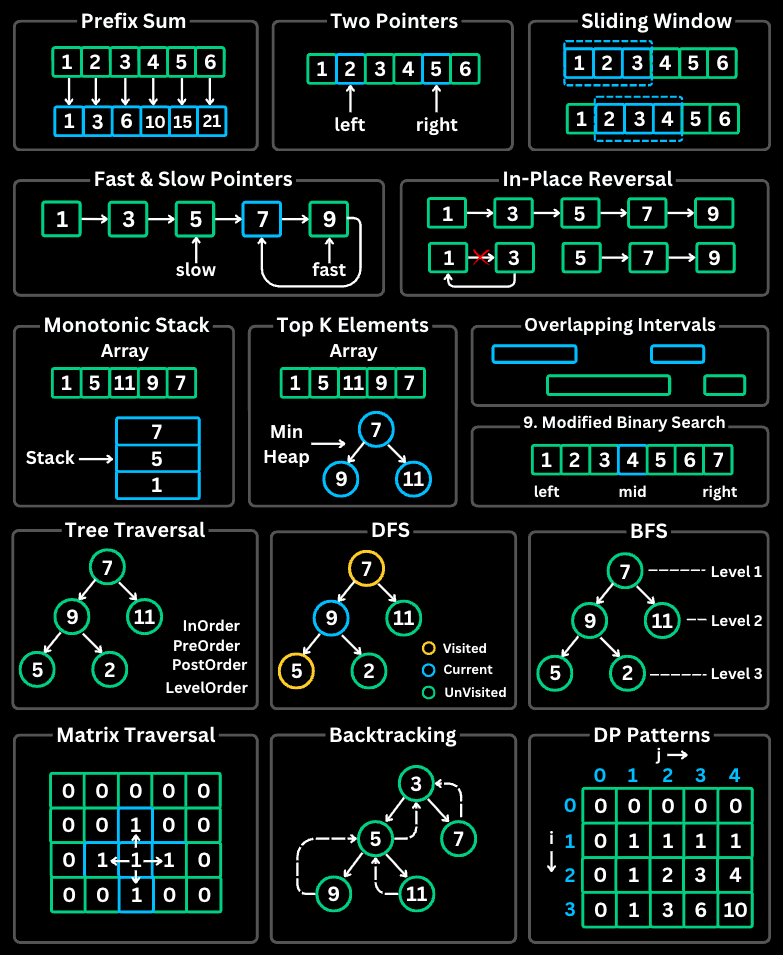
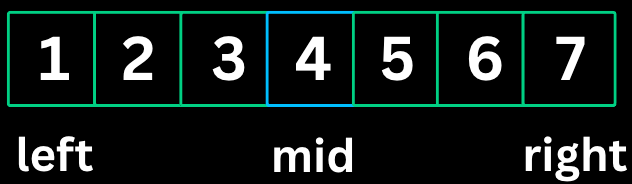
1. Prefix Sum

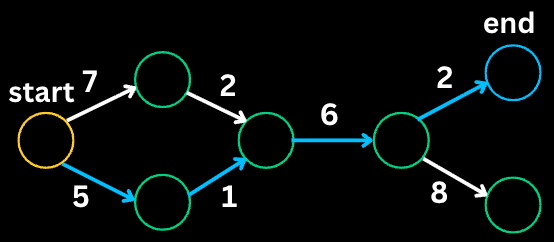
The Prefix Sum pattern involves preprocessing an array to create a new array where each element at index i represents the sum of all elements from the start up to i. This allows for O(1) sum queries on any subarray.

When to use

• Multiple sum queries on subarrays

• Finding subarrays with a target sum

• Calculating cumulative totals

Template

// Build prefix sum array
int[] prefix = new int[n + 1];
for (int i = 0; i < n; i++) {
    prefix[i + 1] = prefix[i] + nums[i];
}

// Query sum of range [left, right]
int rangeSum = prefix[right + 1] - prefix[left];

Sample Problem

Range Sum Query: Given an array nums, answer multiple queries about the sum of elements within a specific range [i, j].

Example:

• Input: nums = [1, 2, 3, 4, 5, 6], i = 1, j = 3

• Output: 9

Step-by-Step Walkthrough:

nums = [1, 2, 3, 4, 5, 6]

Step 1: Build prefix sum array
  prefix[0] = 0
  prefix[1] = 0 + 1 = 1
  prefix[2] = 1 + 2 = 3
  prefix[3] = 3 + 3 = 6
  prefix[4] = 6 + 4 = 10
  prefix[5] = 10 + 5 = 15
  prefix[6] = 15 + 6 = 21

  prefix = [0, 1, 3, 6, 10, 15, 21]

Step 2: Query sum for range [1, 3]
  sum = prefix[3 + 1] - prefix[1]
  sum = prefix[4] - prefix[1]
  sum = 10 - 1 = 9

Practice Problems

1. Range Sum Query - Immutable (LeetCode #303)

2. Contiguous Array (LeetCode #525)

3. Subarray Sum Equals K (LeetCode #560)

4. Product of Array Except Self (LeetCode #238)

---

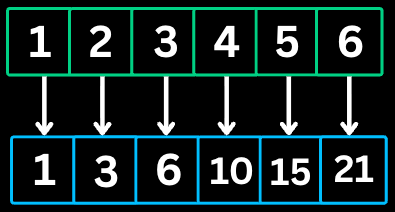
2. Two Pointers

The Two Pointers pattern uses two pointers to traverse an array or list, typically from opposite ends or both moving in the same direction. It reduces time complexity from O(n^2) to O(n) for many problems.

When to use

• Finding pairs in sorted arrays

• Comparing elements from both ends

• Partitioning arrays

• Palindrome checks

Template

// Opposite direction (converging)
int left = 0, right = n - 1;
while (left < right) {
    if (condition_met) {
        // found answer
    } else if (need_larger_sum) {
        left++;
    } else {
        right--;
    }
}

// Same direction
int slow = 0;
for (int fast = 0; fast < n; fast++) {
    if (condition) {
        // process and move slow
        slow++;
    }
}

Sample Problem

Two Sum II: Find two numbers in a sorted array that add up to a target value. Return their indices.

Example:

• Input: nums = [1, 2, 3, 4, 6], target = 6

• Output: [1, 3] (indices of 2 and 4)

Step-by-Step Walkthrough:

nums = [1, 2, 3, 4, 6], target = 6

Step 1: left = 0, right = 4
  sum = nums[0] + nums[4] = 1 + 6 = 7 > 6
  Move right pointer left: right = 3

Step 2: left = 0, right = 3
  sum = nums[0] + nums[3] = 1 + 4 = 5 < 6
  Move left pointer right: left = 1

Step 3: left = 1, right = 3
  sum = nums[1] + nums[3] = 2 + 4 = 6 == target
  Found! Return [1, 3]

Practice Problems

1. Two Sum II - Input Array is Sorted (LeetCode #167)

2. 3Sum (LeetCode #15)

3. Container With Most Water (LeetCode #11)

4. Trapping Rain Water (LeetCode #42)

5. Valid Palindrome (LeetCode #125)

---

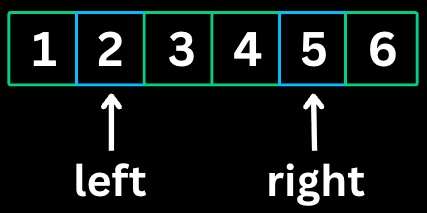
3. Sliding Window

The Sliding Window pattern maintains a window of elements and slides it across the array to find subarrays or substrings that satisfy certain conditions. It avoids recalculating overlapping parts of consecutive windows.

When to use

• Contiguous subarray/substring problems

• Finding maximum/minimum in window of size k

• Longest/shortest substring with certain properties

• Problems involving consecutive elements

Template

// Fixed-size window
int windowSum = 0;
for (int i = 0; i < n; i++) {
    windowSum += nums[i];
    if (i >= k - 1) {
        // process window
        result = Math.max(result, windowSum);
        windowSum -= nums[i - k + 1];
    }
}

// Variable-size window
int left = 0;
for (int right = 0; right < n; right++) {
    // expand window by including nums[right]

    while (window_condition_violated) {
        // shrink window from left
        left++;
    }

    // update result
}

Sample Problem

Maximum Sum Subarray of Size K: Find the maximum sum of any contiguous subarray of size k.

Example:

• Input: nums = [2, 1, 5, 1, 3, 2], k = 3

• Output: 9

Step-by-Step Walkthrough:

nums = [2, 1, 5, 1, 3, 2], k = 3

Step 1: Build initial window [2, 1, 5]
  windowSum = 2 + 1 + 5 = 8
  maxSum = 8

Step 2: Slide window to [1, 5, 1]
  windowSum = 8 - 2 + 1 = 7
  maxSum = max(8, 7) = 8

Step 3: Slide window to [5, 1, 3]
  windowSum = 7 - 1 + 3 = 9
  maxSum = max(8, 9) = 9

Step 4: Slide window to [1, 3, 2]
  windowSum = 9 - 5 + 2 = 6
  maxSum = max(9, 6) = 9

Result: 9

Practice Problems

1. Maximum Average Subarray I (LeetCode #643)

2. Longest Substring Without Repeating Characters (LeetCode #3)

3. Minimum Window Substring (LeetCode #76)

4. Permutation in String (LeetCode #567)

5. Sliding Window Maximum (LeetCode #239)

---

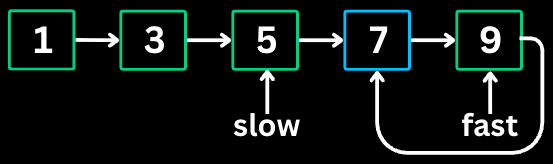
4. Fast & Slow Pointers

The Fast & Slow Pointers pattern (also called Tortoise and Hare) uses two pointers moving at different speeds. When there is a cycle, the fast pointer will eventually meet the slow pointer.

When to use

• Detecting cycles in linked lists or arrays

• Finding the middle of a linked list

• Finding the start of a cycle

Template

// Find middle
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
}
return slow; // middle node

// Cycle detection
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;

    if (slow == fast) {
        // cycle detected
        return true;
    }
}
return false; // no cycle

Sample Problem

Linked List Cycle: Detect if a linked list has a cycle.

Example:

• Input: head = [3, 2, 0, -4], tail connects to node index 1

• Output: true

Step-by-Step Walkthrough:

List: 3 -> 2 -> 0 -> -4 -> (back to 2)

Step 1: slow = 3, fast = 3
Step 2: slow = 2, fast = 0
Step 3: slow = 0, fast = 2 (wrapped around)
Step 4: slow = -4, fast = -4

slow == fast, cycle detected!

Practice Problems

1. Linked List Cycle (LeetCode #141)

2. Linked List Cycle II (LeetCode #142)

3. Happy Number (LeetCode #202)

4. Find the Duplicate Number (LeetCode #287)

5. Middle of the Linked List (LeetCode #876)

---

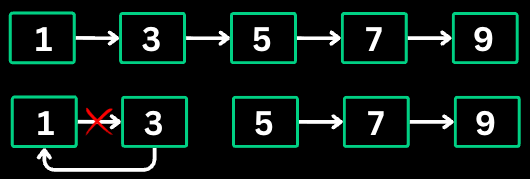
5. LinkedList In-place Reversal

This pattern reverses parts of a linked list without using extra space. It manipulates pointers to reverse the direction of links.

When to use

• Reversing a linked list or portion of it

• Reversing nodes in groups

• Checking for palindromes in linked lists

Template

// Reverse entire list
ListNode prev = null, curr = head;
while (curr != null) {
    ListNode next = curr.next;
    curr.next = prev;
    prev = curr;
    curr = next;
}
return prev; // new head

Sample Problem

Reverse Linked List II: Reverse the nodes of a linked list from position m to n.

Example:

• Input: head = [1, 2, 3, 4, 5], m = 2, n = 4

• Output: [1, 4, 3, 2, 5]

Step-by-Step Walkthrough:

Original: 1 -> 2 -> 3 -> 4 -> 5
Reverse positions 2 to 4

Step 1: Position prev before node 2
  prev = 1, curr = 2

Step 2: Move 3 after 1
  1 -> 3 -> 2 -> 4 -> 5

Step 3: Move 4 after 1
  1 -> 4 -> 3 -> 2 -> 5

Result: [1, 4, 3, 2, 5]

Practice Problems

1. Reverse Linked List (LeetCode #206)

2. Reverse Linked List II (LeetCode #92)

3. Swap Nodes in Pairs (LeetCode #24)

4. Reverse Nodes in k-Group (LeetCode #25)

5. Palindrome Linked List (LeetCode #234)

---

6. Frequency Counting

The Frequency Counting pattern uses hash maps or arrays to count occurrences of elements. It transforms O(n^2) lookup problems into O(n) by trading space for time.

When to use

• Finding duplicates or unique elements

• Checking if two collections have same elements

• Finding elements that appear k times

• Anagram problems

Template

// Using HashMap
Map<Integer, Integer> freq = new HashMap<>();
for (int num : nums) {
    freq.put(num, freq.getOrDefault(num, 0) + 1);
}

// Using array (when range is known)
int[] freq = new int[26]; // for lowercase letters
for (char c : str.toCharArray()) {
    freq[c - 'a']++;
}

// Finding element with specific frequency
for (Map.Entry<Integer, Integer> entry : freq.entrySet()) {
    if (entry.getValue() == target) {
        return entry.getKey();
    }
}

Sample Problem

Valid Anagram: Given two strings s and t, return true if t is an anagram of s.

Example:

• Input: s = "anagram", t = "nagaram"

• Output: true

Step-by-Step Walkthrough:

s = "anagram", t = "nagaram"

Step 1: Count frequencies in s
  freq = {a: 3, n: 1, g: 1, r: 1, m: 1}

Step 2: Decrement frequencies using t
  't' -> n: freq[n] = 1 - 1 = 0
  't' -> a: freq[a] = 3 - 1 = 2
  't' -> g: freq[g] = 1 - 1 = 0
  't' -> a: freq[a] = 2 - 1 = 1
  't' -> r: freq[r] = 1 - 1 = 0
  't' -> a: freq[a] = 1 - 1 = 0
  't' -> m: freq[m] = 1 - 1 = 0

Step 3: Check all frequencies are 0
  freq = {a: 0, n: 0, g: 0, r: 0, m: 0}
  All zero -> Return true

Practice Problems

1. Valid Anagram (LeetCode #242)

2. Group Anagrams (LeetCode #49)

3. Top K Frequent Elements (LeetCode #347)

4. First Unique Character in a String (LeetCode #387)

---

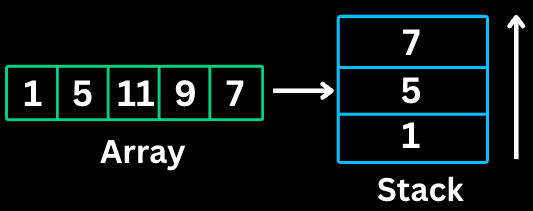
7. Monotonic Stack

A Monotonic Stack maintains elements in either increasing or decreasing order. As you iterate, you pop elements that violate the order, which reveals relationships between elements.

When to use

• Finding the next greater/smaller element

• Finding previous greater/smaller element

• Problems involving spans or ranges

• Histogram problems

Template

/// Next Greater Element (decreasing stack)
int[] result = new int[n];
Arrays.fill(result, -1);
Stack<Integer> stack = new Stack<>(); // stores indices

for (int i = 0; i < n; i++) {
    while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) {
        int idx = stack.pop();
        result[idx] = nums[i];
    }
    stack.push(i);
}

Sample Problem

Next Greater Element: For each element in an array, find the next greater element. Output -1 if none exists.

Example:

• Input: nums = [2, 1, 2, 4, 3]

• Output: [4, 2, 4, -1, -1]

Step-by-Step Walkthrough:

nums = [2, 1, 2, 4, 3]
result = [-1, -1, -1, -1, -1]
stack = []

Step 1: i = 0, nums[0] = 2
  stack is empty, push 0
  stack = [0]

Step 2: i = 1, nums[1] = 1
  1 < nums[0]=2, push 1
  stack = [0, 1]

Step 3: i = 2, nums[2] = 2
  2 > nums[1]=1, pop 1, result[1] = 2
  2 <= nums[0]=2, push 2
  stack = [0, 2], result = [-1, 2, -1, -1, -1]

Step 4: i = 3, nums[3] = 4
  4 > nums[2]=2, pop 2, result[2] = 4
  4 > nums[0]=2, pop 0, result[0] = 4
  push 3
  stack = [3], result = [4, 2, 4, -1, -1]

Step 5: i = 4, nums[4] = 3
  3 < nums[3]=4, push 4
  stack = [3, 4]

Result: [4, 2, 4, -1, -1]

Practice Problems

1. Next Greater Element I (LeetCode #496)

2. Daily Temperatures (LeetCode #739)

3. Largest Rectangle in Histogram (LeetCode #84)

4. Trapping Rain Water (LeetCode #42)

5. Online Stock Span (LeetCode #901)

---

8. Bit Manipulation

Bit manipulation uses binary operations (AND, OR, XOR, NOT, shifts) to solve problems efficiently. XOR is particularly useful since a ^ a = 0 and a ^ 0 = a.

When to use

• Finding unique numbers (XOR)

• Checking power of 2

• Counting bits

• Generating subsets using bit masks

• Space optimization

Template

// Basic operations
int and = a & b;        // both bits 1
int or = a | b;         // either bit 1
int xor = a ^ b;        // bits different
int not = ~a;           // flip bits
int leftShift = a << n; // multiply by 2^n
int rightShift = a >> n;// divide by 2^n

// Check if bit i is set
boolean isSet = (n & (1 << i)) != 0;

// Set bit i
n = n | (1 << i);

// Clear bit i
n = n & ~(1 << i);

// Toggle bit i
n = n ^ (1 << i);

// Check if power of 2
boolean isPowerOf2 = (n > 0) && ((n & (n - 1)) == 0);

// Count set bits
int count = 0;
while (n > 0) {
    count += n & 1;
    n >>= 1;
}
// Or: Integer.bitCount(n);

// Find single number (XOR all elements)
int single = 0;
for (int num : nums) {
    single ^= num;
}

Practice Problems

1. Single Number (LeetCode #136)

2. Number of 1 Bits (LeetCode #191)

3. Counting Bits (LeetCode #338)

4. Power of Two (LeetCode #231)

5. Missing Number (LeetCode #268)

---

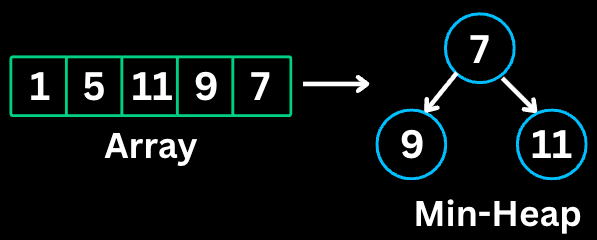
9. Top ‘K’ Elements

This pattern finds the k largest or smallest elements using heaps (priority queues). A min-heap of size k keeps track of k largest elements, and a max-heap keeps k smallest.

When to use

• Finding k largest/smallest elements

• Finding kth largest/smallest element

• Finding k most/least frequent elements

• Merging k sorted lists

Template

// K largest elements using min-heap
PriorityQueue<Integer> minHeap = new PriorityQueue<>();

for (int num : nums) {
    minHeap.offer(num);
    if (minHeap.size() > k) {
        minHeap.poll(); // remove smallest
    }
}
// minHeap now contains k largest elements
// minHeap.peek() is the kth largest

Sample Problem

Kth Largest Element: Find the kth largest element in an unsorted array.

Example:

• Input: nums = [3, 2, 1, 5, 6, 4], k = 2

• Output: 5

Step-by-Step Walkthrough:

nums = [3, 2, 1, 5, 6, 4], k = 2
Using min-heap of size k

Step 1: num = 3
  heap = [3]

Step 2: num = 2
  heap = [2, 3]

Step 3: num = 1
  heap = [1, 3, 2], size > k
  poll smallest: heap = [2, 3]

Step 4: num = 5
  heap = [2, 3, 5], size > k
  poll smallest: heap = [3, 5]

Step 5: num = 6
  heap = [3, 5, 6], size > k
  poll smallest: heap = [5, 6]

Step 6: num = 4
  heap = [4, 6, 5], size > k
  poll smallest: heap = [5, 6]

heap.peek() = 5 (kth largest)

Practice Problems

1. Kth Largest Element in an Array (LeetCode #215)

2. Top K Frequent Elements (LeetCode #347)

3. K Closest Points to Origin (LeetCode #973)

4. Find K Pairs with Smallest Sums (LeetCode #373)

5. Kth Largest Element in a Stream (LeetCode #703)

---

10. Overlapping Intervals

This pattern handles problems involving intervals that may overlap. The key insight is that after sorting by start time, two intervals [a, b] and [c, d] overlap if b >= c.

When to use

• Merging overlapping intervals

• Finding interval intersections

• Scheduling problems (meeting rooms)

• Inserting into sorted intervals

Template

// Sort by start time
Arrays.sort(intervals, (a, b) -> a[0] - b[0]);

// Merge overlapping intervals
List<int[]> merged = new ArrayList<>();
for (int[] interval : intervals) {
    if (merged.isEmpty() || merged.get(merged.size() - 1)[1] < interval[0]) {
        // no overlap, add new interval
        merged.add(interval);
    } else {
        // overlap, merge by extending end time
        merged.get(merged.size() - 1)[1] =
            Math.max(merged.get(merged.size() - 1)[1], interval[1]);
    }
}

Sample Problem

Merge Intervals: Given a collection of intervals, merge all overlapping intervals.

Example:

• Input: intervals = [[1,3], [2,6], [8,10], [15,18]]

• Output: [[1,6], [8,10], [15,18]]

Step-by-Step Walkthrough:

intervals = [[1,3], [2,6], [8,10], [15,18]]
(Already sorted by start time)

Step 1: interval = [1,3]
  merged is empty, add [1,3]
  merged = [[1,3]]

Step 2: interval = [2,6]
  last = [1,3], start = 2 <= end = 3
  Overlap! Merge: end = max(3, 6) = 6
  merged = [[1,6]]

Step 3: interval = [8,10]
  last = [1,6], start = 8 > end = 6
  No overlap, add [8,10]
  merged = [[1,6], [8,10]]

Step 4: interval = [15,18]
  last = [8,10], start = 15 > end = 10
  No overlap, add [15,18]
  merged = [[1,6], [8,10], [15,18]]

Practice Problems

1. Merge Intervals (LeetCode #56)

2. Insert Interval (LeetCode #57)

3. Non-overlapping Intervals (LeetCode #435)

4. Meeting Rooms (LeetCode #252)

5. Meeting Rooms II (LeetCode #253)

---

11. Modified Binary Search

This pattern adapts binary search to handle rotated arrays, finding boundaries, or searching for conditions rather than exact values.

When to use

• Searching in rotated sorted arrays

• Finding first/last occurrence of element

• Finding minimum/maximum satisfying a condition

• Peak finding problems

Template

// Standard binary search
int left = 0, right = n - 1;
while (left <= right) {
    int mid = left + (right - left) / 2;
    if (nums[mid] == target) return mid;
    else if (nums[mid] < target) left = mid + 1;
    else right = mid - 1;
}

// Find first occurrence
while (left < right) {
    int mid = left + (right - left) / 2;
    if (condition(mid)) right = mid;
    else left = mid + 1;
}

Sample Problem

Search in Rotated Sorted Array: Search for a target in a rotated sorted array.

Example:

• Input: nums = [4, 5, 6, 7, 0, 1, 2], target = 0

• Output: 4

Step-by-Step Walkthrough:

nums = [4, 5, 6, 7, 0, 1, 2], target = 0

Step 1: left = 0, right = 6, mid = 3
  nums[mid] = 7 != 0
  nums[left] = 4 <= nums[mid] = 7 (left half sorted)
  target = 0 not in [4, 7), search right
  left = 4

Step 2: left = 4, right = 6, mid = 5
  nums[mid] = 1 != 0
  nums[left] = 0 <= nums[mid] = 1 (left half sorted)
  target = 0 in [0, 1), search left
  right = 4

Step 3: left = 4, right = 4, mid = 4
  nums[mid] = 0 == target
  Found at index 4!

Practice Problems

1. Search in Rotated Sorted Array (LeetCode #33)

2. Find Minimum in Rotated Sorted Array (LeetCode #153)

3. Search a 2D Matrix (LeetCode #74)

4. Find Peak Element (LeetCode #162)

5. First Bad Version (LeetCode #278)

---

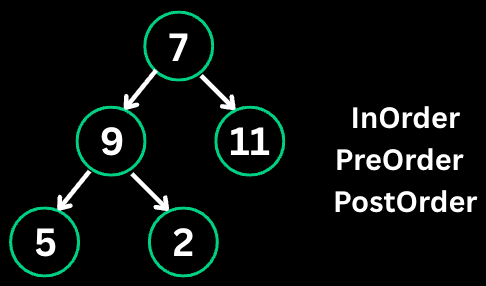
12. Binary Tree Traversal

Binary Tree Traversal visits all nodes in a specific order. The three main orders are preorder (root-left-right), inorder (left-root-right), and postorder (left-right-root).

When to use

• Processing tree nodes in specific order

• Building trees from traversals

• BST operations (inorder gives sorted order)

• Tree serialization/deserialization

Template

// Preorder (Root -> Left -> Right)
void preorder(TreeNode node) {
    if (node == null) return;
    process(node);        // visit root
    preorder(node.left);  // left subtree
    preorder(node.right); // right subtree
}

// Inorder (Left -> Root -> Right)
void inorder(TreeNode node) {
    if (node == null) return;
    inorder(node.left);   // left subtree
    process(node);        // visit root
    inorder(node.right);  // right subtree
}

// Postorder (Left -> Right -> Root)
void postorder(TreeNode node) {
    if (node == null) return;
    postorder(node.left);  // left subtree
    postorder(node.right); // right subtree
    process(node);         // visit root
}

Sample Problem

Inorder Traversal: Return the inorder traversal of a binary tree.

Example:

• Input: Tree with root = [1, null, 2, 3]

• Output: [1, 3, 2]

Step-by-Step Walkthrough:

Tree:
    1
     \
      2
     /
    3

Inorder: Left -> Root -> Right

Step 1: Start at 1
  No left child, visit 1
  result = [1]

Step 2: Go to right child 2
  Has left child 3, go left

Step 3: At node 3
  No left child, visit 3
  result = [1, 3]
  No right child, backtrack

Step 4: Back at node 2
  Left done, visit 2
  result = [1, 3, 2]
  No right child

Done: [1, 3, 2]

Practice Problems

1. Binary Tree Inorder Traversal (LeetCode #94)

2. Binary Tree Preorder Traversal (LeetCode #144)

3. Binary Tree Postorder Traversal (LeetCode #145)

4. Kth Smallest Element in a BST (LeetCode #230)

5. Validate Binary Search Tree (LeetCode #98)

---

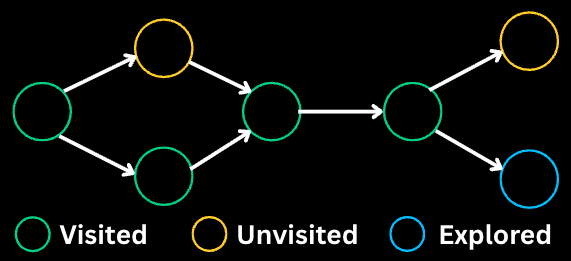
13. Depth-First Search (DFS)

DFS explores as deep as possible along each branch before backtracking. It uses a stack (or recursion) to remember which nodes to visit next.

When to use

• Exploring all paths in a tree/graph

• Finding connected components

• Detecting cycles

• Topological sorting

• Path finding when all paths matter

Template

// DFS on a graph - visited tracking required
void dfs(int node, boolean[] visited, List<List<Integer>> graph) {
    visited[node] = true;

    // Process current node
    process(node);

    // Explore unvisited neighbors
    for (int neighbor : graph.get(node)) {
        if (!visited[neighbor]) {
            dfs(neighbor, visited, graph);
        }
    }
}

Sample Problem

Path Sum: Determine if the tree has a root-to-leaf path where values sum to a target.

Example:

• Input: root = [5, 4, 8, 11, null, 13, 4, 7, 2], targetSum = 22

• Output: true (path: 5 -> 4 -> 11 -> 2)

Step-by-Step Walkthrough:

Tree:
        5
       / \
      4   8
     /   / \
    11  13  4
   /  \      \
  7    2      1

Target = 22

DFS Path 1: 5 -> 4 -> 11 -> 7
  Sum = 5 + 4 + 11 + 7 = 27 != 22

DFS Path 2: 5 -> 4 -> 11 -> 2
  Sum = 5 + 4 + 11 + 2 = 22 == target
  Found! Return true

Practice Problems

1. Path Sum (LeetCode #112)

2. Path Sum II (LeetCode #113)

3. Clone Graph (LeetCode #133)

4. Course Schedule II (LeetCode #210)

5. Number of Islands (LeetCode #200)

---

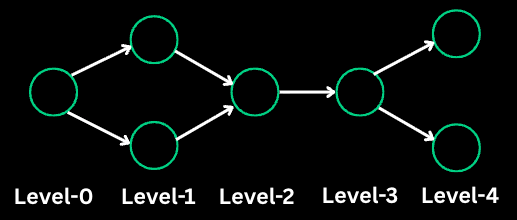
14. Breadth-First Search (BFS)

BFS explores nodes level by level, visiting all neighbors before moving deeper. It uses a queue and guarantees the shortest path in unweighted graphs.

When to use

• Finding shortest path (unweighted)

• Level-order traversal

• Finding all nodes at distance k

• Spreading problems (rotting oranges, walls and gates)

Template

public void bfs(Node start) {
    // Handle edge case
    if (start == null) return;

    // Initialize queue and visited set
    Queue<Node> queue = new LinkedList<>();
    Set<Node> visited = new HashSet<>();

    // Add starting node
    queue.offer(start);
    visited.add(start);

    // Process nodes level by level
    while (!queue.isEmpty()) {
        Node current = queue.poll();

        // Process the current node
        process(current);

        // Add unvisited neighbors to queue
        for (Node neighbor : current.getNeighbors()) {
            if (!visited.contains(neighbor)) {
                visited.add(neighbor);
                queue.offer(neighbor);
            }
        }
    }
}

Sample Problem

Level Order Traversal: Return the level order traversal of a binary tree.

Example:

• Input: root = [3, 9, 20, null, null, 15, 7]

• Output: [[3], [9, 20], [15, 7]]

Step-by-Step Walkthrough:

Tree:
    3
   / \
  9  20
    /  \
   15   7

Step 1: Level 0
  queue = [3]
  Process 3, add children 9, 20
  result = [[3]]

Step 2: Level 1
  queue = [9, 20]
  Process 9 (no children)
  Process 20, add children 15, 7
  result = [[3], [9, 20]]

Step 3: Level 2
  queue = [15, 7]
  Process 15 (no children)
  Process 7 (no children)
  result = [[3], [9, 20], [15, 7]]

Practice Problems

1. Binary Tree Level Order Traversal (LeetCode #102)

2. Rotting Oranges (LeetCode #994)

3. Word Ladder (LeetCode #127)

4. Minimum Depth of Binary Tree (LeetCode #111)

5. Walls and Gates (LeetCode #286)

---

15. Shortest Path

Shortest path algorithms find the minimum distance between nodes. Dijkstra’s works for weighted graphs with non-negative weights, while Bellman-Ford handles negative weights.

When to use

• Finding minimum cost/distance paths

• Network routing problems

• Weighted graph traversal

• Problems with varying edge costs

Template

// Dijkstra's Algorithm using Priority Queue
int[] dist = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[source] = 0;

// PQ: (distance, node)
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] - b[0]);
pq.offer(new int[]{0, source});

while (!pq.isEmpty()) {
    int[] curr = pq.poll();
    int d = curr[0], node = curr[1];

    if (d > dist[node]) continue; // already processed

    for (int[] edge : graph.get(node)) {
        int neighbor = edge[0], weight = edge[1];
        int newDist = dist[node] + weight;

        if (newDist < dist[neighbor]) {
            dist[neighbor] = newDist;
            pq.offer(new int[]{newDist, neighbor});
        }
    }
}

Sample Problem

Network Delay Time: Find the time it takes for a signal to reach all nodes from a source node.

Example:

• Input: times = [[2,1,1], [2,3,1], [3,4,1]], n = 4, k = 2

• Output: 2

Step-by-Step Walkthrough:

Graph: 2 --(1)--> 1
       2 --(1)--> 3 --(1)--> 4
Source: node 2

Initial: dist = [INF, INF, 0, INF, INF] (1-indexed)
         pq = [(0, 2)]

Step 1: Process (0, 2)
  Neighbor 1: dist[1] = 0 + 1 = 1
  Neighbor 3: dist[3] = 0 + 1 = 1
  pq = [(1, 1), (1, 3)]

Step 2: Process (1, 1)
  No outgoing edges
  pq = [(1, 3)]

Step 3: Process (1, 3)
  Neighbor 4: dist[4] = 1 + 1 = 2
  pq = [(2, 4)]

Step 4: Process (2, 4)
  No outgoing edges

dist = [INF, 1, 0, 1, 2]
Max distance = 2

Practice Problems

1. Network Delay Time (LeetCode #743)

2. Cheapest Flights Within K Stops (LeetCode #787)

3. Path with Maximum Probability (LeetCode #1514)

4. Swim in Rising Water (LeetCode #778)

5. Path with Minimum Effort (LeetCode #1631)

---

16. Matrix Traversal

Matrix traversal uses DFS or BFS to explore 2D grids. The key is handling 4-directional (or 8-directional) movement and boundary checks.

When to use

• Grid-based problems (islands, regions)

• Flood fill algorithms

• Finding connected components in 2D

• Path finding in mazes

Template

// Direction arrays for 4 directions
int[] dx = {0, 0, 1, -1};
int[] dy = {1, -1, 0, 0};

// DFS on matrix
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
    int m = grid.length, n = grid[0].length;

    // boundary and validity check
    if (i < 0 || i >= m || j < 0 || j >= n) return;
    if (visited[i][j] || grid[i][j] == 0) return;

    visited[i][j] = true;
    // process cell

    // explore 4 directions
    for (int d = 0; d < 4; d++) {
        dfs(grid, i + dx[d], j + dy[d], visited);
    }
}

// BFS on matrix
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{startRow, startCol});
visited[startRow][startCol] = true;

while (!queue.isEmpty()) {
    int[] cell = queue.poll();
    int i = cell[0], j = cell[1];

    for (int d = 0; d < 4; d++) {
        int ni = i + dx[d], nj = j + dy[d];
        if (ni >= 0 && ni < m && nj >= 0 && nj < n
            && !visited[ni][nj] && grid[ni][nj] == 1) {
            visited[ni][nj] = true;
            queue.offer(new int[]{ni, nj});
        }
    }
}

Sample Problem

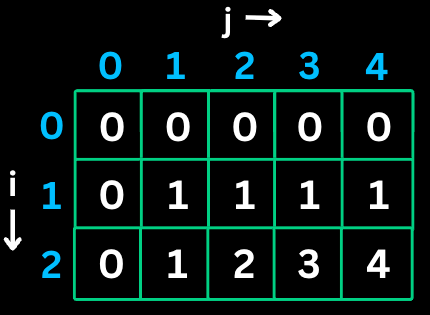
Number of Islands: Count the number of islands (connected 1s) in a 2D grid.

Example:

• Input:

grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]

• Output: 3

Step-by-Step Walkthrough:

Grid:
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

Step 1: Find '1' at (0,0)
  DFS marks connected cells: (0,0), (0,1), (1,0), (1,1)
  islands = 1

Step 2: Find '1' at (2,2)
  DFS marks: (2,2)
  islands = 2

Step 3: Find '1' at (3,3)
  DFS marks connected cells: (3,3), (3,4)
  islands = 3

Result: 3 islands

Practice Problems

1. Number of Islands (LeetCode #200)

2. Flood Fill (LeetCode #733)

3. Surrounded Regions (LeetCode #130)

4. Max Area of Island (LeetCode #695)

5. Pacific Atlantic Water Flow (LeetCode #417)

---

17. Backtracking

Backtracking explores all possible solutions by making choices, and undoes (backtracks) when a path leads to an invalid solution. It builds solutions incrementally.

When to use

• Generating all permutations/combinations/subsets

• Solving constraint satisfaction problems (N-Queens, Sudoku)

• Finding all paths meeting certain criteria

• String partitioning problems

Template

public void backtrack(State state, Choices choices, Results results) {
    // Base case: Is this a complete solution?
    if (isComplete(state)) {
        results.add(copy(state));  // Store the solution
        return;
    }

    // Recursive case: Try each available choice
    for (Choice choice : getAvailableChoices(state, choices)) {
        // 1. CHOOSE: Make the choice
        makeChoice(state, choice);

        // 2. EXPLORE: Recursively explore with this choice
        backtrack(state, choices, results);

        // 3. UNCHOOSE: Undo the choice (backtrack)
        undoChoice(state, choice);
    }
}

Sample Problem

Subsets: Generate all possible subsets of an array.

Example:

• Input: nums = [1, 2, 3]

• Output: [[], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3]]

Step-by-Step Walkthrough:

nums = [1, 2, 3]

backtrack([], start=0)
  add [] to result

  i=0: choose 1 -> [1]
    backtrack([1], start=1)
      add [1] to result

      i=1: choose 2 -> [1,2]
        backtrack([1,2], start=2)
          add [1,2] to result

          i=2: choose 3 -> [1,2,3]
            backtrack([1,2,3], start=3)
              add [1,2,3] to result
            unchoose 3 -> [1,2]
        unchoose 2 -> [1]

      i=2: choose 3 -> [1,3]
        backtrack([1,3], start=3)
          add [1,3] to result
        unchoose 3 -> [1]
    unchoose 1 -> []

  i=1: choose 2 -> [2]
    ...similar process

Result: [[], [1], [1,2], [1,2,3], [1,3], [2], [2,3], [3]]

Practice Problems

1. Subsets (LeetCode #78)

2. Permutations (LeetCode #46)

3. Combination Sum (LeetCode #39)

4. N-Queens (LeetCode #51)

5. Word Search (LeetCode #79)

---

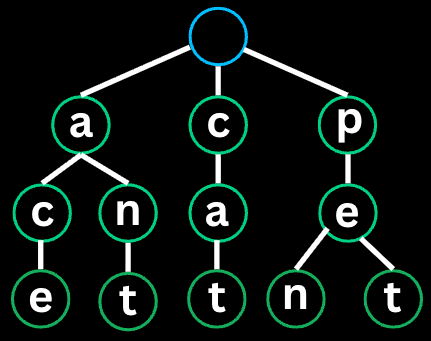
18. Prefix Search (Trie)

A Trie (prefix tree) stores strings character by character, allowing efficient prefix lookups. Each node represents a character, and paths from root to nodes represent prefixes.

When to use

• Autocomplete and search suggestions

• Spell checking

• IP routing (longest prefix match)

• Word games (finding valid words)

Template

class TrieNode {
    TrieNode[] children = new TrieNode[26];
    boolean isEndOfWord = false;
}

class Trie {
    TrieNode root = new TrieNode();

    void insert(String word) {
        TrieNode node = root;
        for (char c : word.toCharArray()) {
            int idx = c - 'a';
            if (node.children[idx] == null) {
                node.children[idx] = new TrieNode();
            }
            node = node.children[idx];
        }
        node.isEndOfWord = true;
    }

    boolean search(String word) {
        TrieNode node = searchPrefix(word);
        return node != null && node.isEndOfWord;
    }

    boolean startsWith(String prefix) {
        return searchPrefix(prefix) != null;
    }

    private TrieNode searchPrefix(String prefix) {
        TrieNode node = root;
        for (char c : prefix.toCharArray()) {
            int idx = c - 'a';
            if (node.children[idx] == null) return null;
            node = node.children[idx];
        }
        return node;
    }
}

Sample Problem

Implement Trie: Implement a trie with insert, search, and startsWith methods.

Example:

Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true

Step-by-Step Walkthrough:

Insert "apple":

  root
   |
   a (idx=0)
   |
   p (idx=15)
   |
   p (idx=15)
   |
   l (idx=11)
   |
   e (idx=4, isEndOfWord=true)

Search "apple":
  Traverse: a -> p -> p -> l -> e
  Node exists and isEndOfWord = true
  Return true

Search "app":
  Traverse: a -> p -> p
  Node exists but isEndOfWord = false
  Return false

StartsWith "app":
  Traverse: a -> p -> p
  Node exists (prefix found)
  Return true

Practice Problems

1. Implement Trie (LeetCode #208)

2. Word Search II (LeetCode #212)

3. Design Add and Search Words Data Structure (LeetCode #211)

4. Replace Words (LeetCode #648)

5. Longest Word in Dictionary (LeetCode #720)

---

19. Greedy

Greedy algorithms make locally optimal choices at each step, hoping to find a global optimum. They work when local optimal choices lead to global optimal solutions.

When to use

• Optimization problems with greedy choice property

• Interval scheduling

• Huffman coding

• Activity selection

• When proof by exchange argument works

Template

public Result solveGreedy(Input input) {
    // Step 1: Sort or organize input (if needed)
    sort(input, byGreedyCriterion);

    // Step 2: Initialize result and tracking variables
    Result result = initialResult();
    State state = initialState();

    // Step 3: Iterate and make greedy choices
    for (Element element : input) {
        if (canInclude(element, state)) {
            // Make the greedy choice
            result = update(result, element);
            state = updateState(state, element);
        }
    }

    return result;
}

Sample Problem

Jump Game: Determine if you can reach the last index starting from index 0.

Example:

• Input: nums = [2, 3, 1, 1, 4]

• Output: true

Step-by-Step Walkthrough:

nums = [2, 3, 1, 1, 4]

Track maxReach (farthest index we can reach)

Step 1: i = 0, nums[0] = 2
  maxReach = max(0, 0 + 2) = 2

Step 2: i = 1, nums[1] = 3
  i <= maxReach (1 <= 2)
  maxReach = max(2, 1 + 3) = 4

Step 3: i = 2, nums[2] = 1
  i <= maxReach (2 <= 4)
  maxReach = max(4, 2 + 1) = 4

Step 4: i = 3, nums[3] = 1
  i <= maxReach (3 <= 4)
  maxReach = max(4, 3 + 1) = 4

maxReach = 4 >= last index (4)
Return true

Practice Problems

1. Jump Game (LeetCode #55)

2. Jump Game II (LeetCode #45)

3. Gas Station (LeetCode #134)

4. Task Scheduler (LeetCode #621)

5. Partition Labels (LeetCode #763)

---

20. Dynamic Programming Patterns

Dynamic Programming (DP) solves problems by breaking them into overlapping subproblems and storing results to avoid recomputation. It works when problems have optimal substructure.

When to use

• Problems with overlapping subproblems

• Optimization (min/max) problems

• Counting problems (number of ways)

• Decision problems (can we achieve X?)

Common DP Patterns

1. Fibonacci Pattern (1D DP with previous states)

2. 0/1 Knapsack (include or exclude each item)

3. Longest Common Subsequence (2D DP on two sequences)

4. Longest Increasing Subsequence

You can find more DP patterns and how to approach them in this article.

Sample Problem

Climbing Stairs: Find the number of ways to climb n stairs, taking 1 or 2 steps at a time.

Example:

• Input: n = 4

• Output: 5

Step-by-Step Walkthrough:

n = 4

dp[i] = number of ways to reach step i
dp[i] = dp[i-1] + dp[i-2]
(we can reach step i from step i-1 or step i-2)

Base cases:
  dp[0] = 1 (one way to stay at ground)
  dp[1] = 1 (one way: take 1 step)

Step 2: dp[2] = dp[1] + dp[0] = 1 + 1 = 2
  Ways: [1,1], [2]

Step 3: dp[3] = dp[2] + dp[1] = 2 + 1 = 3
  Ways: [1,1,1], [1,2], [2,1]

Step 4: dp[4] = dp[3] + dp[2] = 3 + 2 = 5
  Ways: [1,1,1,1], [1,1,2], [1,2,1], [2,1,1], [2,2]

Result: 5 ways

Practice Problems

1. Climbing Stairs (LeetCode #70)

2. House Robber (LeetCode #198)

3. Coin Change (LeetCode #322)

4. Longest Common Subsequence (LeetCode #1143)

5. Longest Increasing Subsequence (LeetCode #300)

6. Partition Equal Subset Sum (LeetCode #416)

7. Edit Distance (LeetCode #72)

---

That’s it. Thanks for reading!

I’ve put together many more patterns and problems on my website. You can explore them here: algomaster.io

If this article helped you, give it a like and share it with others.